Science and Evidence: Falsifiability and Prediction
How is it that many people insist that there is no evidence for the theory of evolution or the Big Bang theory, yet scientists will insist that there is massive evidence for these theories? The controversy comes from a misunderstanding of what constitutes scientific evidence. Laymen tend to think that unless we can observe things directly over and over again right in front of our eyes, we have no business claiming that there is scientific proof. So when the subject of evolution comes up, it is natural for people to complain that what happens in the past is not something we can observe directly over and over again. There must be a catch somewhere, otherwise so many evolutionary biologists would not be employed. The answer lies in how the pioneers of science figured out how we can extend our powers of observation and verification far beyond the laboratory and far back in deep time.
Direct Observation
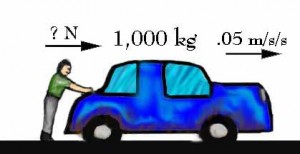
What comes to mind with the term Direct Observation is a typical series of laboratory experiments that allow us to characterize something repeatable. A good example of this would be Newton’s Laws of Motion. Consider Newton’s Law, F = MA. This formula predicts how fast a given mass M will accelerate A when subject to a given force F1. It is easy to see that one could perform any number of experiments with forces and masses and directly observe the acceleration.
So F = MA for things that we can experiment on directly is easily confirmed. The important point here, though, is that we confirm F = MA by seeing how well its prediction for acceleration matches what we observe in nature. In other words, in science, we measure the truth of a hypothesis by how accurately it predicts nature. So it is important that a scientific hypothesis make very testable predictions so that we can either confirm them or falsify them. Otherwise all we have is someone’s untestable opinion.
F = MA satisfies that criteria because it makes very precise predictions. And consider that the more precise the prediction from a hypothesis the more it is at risk for being proven wrong. The more those precise predictions continues to not be proven wrong, the more we can gain confidence in it. So science would say that F = MA is highly falsifiable2, or that it produces highly falsifiable predictions.
What we want is a hypothesis that takes great risk in making very testable precise predictions and manages to not fail in situation after situation. This doesn’t help us with evolution yet, however, because we cannot make direct observations with laboratory experiments to confirm that a hypothesis like humans and chimpanzees come from a common ancestor.
Since evolutionary biologists say that this split from a common ancestor happened some 5 million years ago, it doesn’t seem like it is directly observable. And it doesn’t seem like the hypothesis, “Humans and chimpanzees come from a common ancestor”, makes very precise predictions. What would you test for that hypothesis? No falsifiable prediction means no science yet. And yet, science still insists that evolution makes all kinds of predictions that are extremely testable. And that a lot of evidence for it has accumulated over the last 150 years. There must be something more to scientific theories than direct observation.
Indirect Observation
So lets examine how science solved this problem some 500 years ago. Consider that when Newton offered his laws of motion and gravity, he declared them to be universal. In other words, he declared that the laws of motion and gravity apply to all objects in the universe. Now this is taking on a lot more risk it would seem, but from my definition in the previous section, it appears that it does so without the ability for us to test it. It could be making a precise prediction but how can we test F = MA, for example, on something like the planet Jupiter. The problem is that we cannot go to Jupiter, apply different forces to it and measure its acceleration. So it would seem that the prediction from F = MA is not testable or falsifiable because of a practical problem.
One might conclude that we cannot confirm that F = MA can take that risky leap from objects we can mess with in front of us to far off planets and galaxies. It turns out that there is a perfectly good way solve that problem. We can produce a situation where we can gain as much confidence in F = MA as applies to Jupiter as we can for billiard balls on our lab bench. The way we do this is to form a more complex hypothesis out of our simple one in such a way as to coax out new predictions that we can test for Jupiter without actually going there. It works by taking some well tested hypotheses such as the laws of motion and the law of gravity and combing them to form a logical conclusion that can gives us a long range signal to look for.
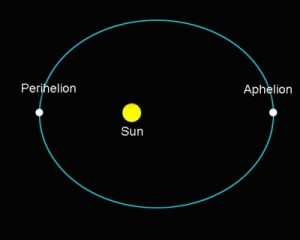
To do this one constructs a logical proof that includes F = MA as a premise and generates a conclusion that makes a testable prediction about something we can observe about the motion of Jupiter from Earth. It turns out that if you take Newton’s Laws of Motion and Newton’s Law of Gravity and combine them mathematically, you can demonstrate that orbiting bodies must follow an elliptical path. This is done in a logical and mathematical proof and the conclusion of elliptical orbits is inescapable. In other words, the math performed on the laws demonstrate that no other shape is possible if gravity is the only thing governing the orbit of the body.
The inescapable conclusion is important because this makes our hypothesis falsifiable. In other words, if our hypothesis uses F = MA as a premise and an elliptical orbit is inescapable, then if we don’t see elliptical orbits our hypothesis is falsified. And that means that one or more of the premises, such as F = MA must be falsified in this situation. The important thing here is that the logic and math that connected elliptical orbits to F = MA has formed a kind of truth pipeline that causes the truth of F = MA to rely on the truth of the conclusion of elliptical orbits. This only works if no other possible conclusion than elliptical orbits can be had from the logic and math. So by making this inescapable logical connection between F = MA and elliptical orbits, we extend our ability to confirm or refute that F = MA is at work for the planet Jupiter. This is important because now our requirement for direct observation in the laboratory is no longer needed.
All we need now is to use the solar system as a laboratory and observe the elliptical orbits of all of our planets and moons. And then we go on to observe them with galaxies and so on. Now if this is not enough to convince us, we can do more math on those laws to produce more inescapable conclusions that predict things about planetary orbits. Once again we combine F = MA with the other laws and some math and logic and we find that if we know the position and velocity of a planet at some point in time To, that we can predict where that planet will be at some point in time, T1. Since our math and logic is done in such a way that the prediction is inescapable (meaning that no other outcome is allowed) then we can simply look at where Jupiter was on March 5, 1972 and predict from that where it will be in the sky tonight. And if that turns out to be accurate, we will have confirmed F = MA for Jupiter in a different way. And we continue to do this, coaxing out every inescapable prediction for the planet Jupiter that are consequences of F = MA and we compare those predictions to the what we observe about Jupiter’s orbit.
Simple Example
The math that leads us to an elliptical orbit is out of the scope of this article, but you are welcome to see it here. Here is a simpler example of combining Newton’s laws to create an inescapable conclusion that creates a testable prediction about nature. Suppose we want to prove that Newton’s Laws insist that all objects fall to earth at the same rate of acceleration regardless of their mass.
| P1. | F = M x A | (Newton’s second law of motion) |
| P2. | F = -F’ | (Newton’s third law of motion: A force on an object produces an equal opposing force.) |
| P3. | F = (Me x M) / (R x R) | (Newton’s law of gravity, where Me is the mass of the earth, M the mass of an object, and R is the distance between their centers of mass). |
| C1. | M x A = (Me x M) ( R x R) | (from P1 through P3, setting the force of gravity equal to the opposing force on the object.) |
| C2. | A = Me / (R x R) | (Cancelling M from both sides.) |
| C3. | Therefore, the acceleration of an object of mass M falling to earth is independent of the mass of the object. | (Notice that M no longer appears in the formula). |
| C4. | Therefore, all objects fall to the earth at the same rate of acceleration regardless of their mass. |
In this proof, P1 through P3 are Newton’s Laws used as premises. C1 through C4 are conclusions drawn from the premises using the rules of algebra. Notice that there is no other possible outcome from this line of logic and math. The mass of the object itself drops out of the equation leaving the objects acceleration totally dependent on the mass of the Earth. Since there is no other possible outcome and if these three laws of motion are governing the fall of objects in a gravitational field, they will all fall at the same rate no matter what their masses are. Now if it turns out that the mass of objects does affect their rate of acceleration while falling, then the hypothesis is falsified. And because of the pipeline of logic that links those three laws to the conclusion, one or more of those laws must also be falsified because we can show that the pipeline itself is correct.
Broken Pipes
What does it look like when the conclusions are not inescapable consequences of the premises. Suppose I want to prove that all swans in my possession are black.
P1. Some swans are black.
P2. I have three swans.
C1. Therefore my three swans are black.
 As you can see here, there is a logic problem. The conclusion is not the only possibility given the two premises. Since P1 says “Some swans…”, we can easily conclude that 0, 1, 2, or 3 of my swans could be black. Notice that if none of my swans are black, it does not disprove P1.
As you can see here, there is a logic problem. The conclusion is not the only possibility given the two premises. Since P1 says “Some swans…”, we can easily conclude that 0, 1, 2, or 3 of my swans could be black. Notice that if none of my swans are black, it does not disprove P1.
So we cannot use any evidence of swan color in my swans to disprove P1. So P1 would be considered an unfalsifiable hypothesis, because there is no way to disprove it.
You could fix it by changing it to “All swans are black.”, in which case any white swans in my collection would falsify it. Or one could be precise about the “some swans” and say that “One out of three swans are black.” This might require us to test a large number of swan, but with enough swans, one could make a case that it is false.
Summary
In summary, here are the important takeaways:
- A hypothesis or theory is considered scientific if it makes testable predictions about nature.
- A scientific hypothesis or theory is only as true as its predictions are accurate.
- Further predictions can be obtained from the premises of a theory by linking the premises to further conclusions through valid inescapable logic.
- The “inescapable” criteria is important because it creates a logical unbreakable causal link between the premises and the conclusion.
- Therefore, if the predictions from the conclusions do not turn out to be accurate, one or more of the premises are in doubt.
Notes
Category: Science and Evidence